Модернизация общеобразовательной школы предполагает ориентацию образования не только на усвоение определенного объема знаний, но и на развитие личности, ее познавательных способностей.
Мощным средством развития, выявления способностей и интересов учащихся являются предметные олимпиады.
Математические олимпиады школьников России имеют большую историю и традицию. Так, в 2024 и 2025 гг. научная и педагогическая общественность будет отмечать 90-летие со времени проведения первой Ленинградской (1934 г.) и Московской (1935 г.) олимпиад школьников по математике.
Значительное продвижение в развитие олимпиад конца XX века принесли новые информационные и коммуникационные технологии. Так, широкую известность через сеть Интернет в России получили Международный конкурс-игра «Кенгуру. Математика для всех», «Русский медвежонок», дистанционная олимпиада «Эйдос», Московский интеллектуальный марафон, турниры Архимеда, математические бои, турниры городов и др. Сегодня принять участие в олимпиаде может совершенно любой школьник. Ежегодно проходят муниципальные, областные, межрегиональные, всероссийские и международные олимпиады школьников. Такие как, «Высшая проба», «Сириус», «Покори Воробьевы горы», «Шаг в будущее» и многие другие олимпиады.
Отмечу также, что в настоящее время учителя школ испытывают нехватку современной методической литературы, предназначенной для работы со способными учащимися по организации и проведению кружковых занятий, олимпиад по математике.
Чаще всего школьники предпочитают олимпиады по алгебре чем по геометрии. Поэтому современному учителю необходимо в своей работе в этом направлении построить такую кружковую работу, где на ряду с задачами алгебры ребята смогли нарешивать и геометрические задачи. Поэтому я поставила перед собой цель собрать самые интересные геометрические задачи, выходящие за пределы учебной программы для учащихся 8-9 классов. Собирались такие задачи годами из разных источников. В своей статье мне хотелось бы показать самые яркие и интересные задачи с решениями. И не только задачи, но и вспомогательные понятия и теоремы, с помощью которых можно быстро и рационально решать олимпиадные задачи по геометрии.
Теорема Фалеса: Если на одной из двух прямых отложить последовательно несколько равных между собой отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Эту теорему школьники затрагивают в школьном курсе, но на факультативе или кружке я даю более общую формулировку этой теоремы о пропорциональности отрезков А1 А2 : В1 В2 = А1 А2 : В1 В2 = и т. д. И предлагаю доказать следующее утверждение, которое вытекает из теоремы Фалеса: если стороны угла пересечь параллельными прямыми, то отношения отрезков на одной стороне угла будет равно отношению отрезков на другой стороне угла.
Доказывается это легко на основе подобия треугольников, и уже после предлагаю применить полученные знания на конкретных задачах.
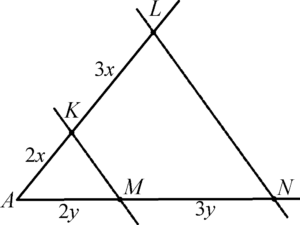
Задача 1: В треугольнике ABC на стороне AC задана
точка B1 , делящая ее в отношении 3 : 2 , считая от A. На отрезке BB1 задана точка K, делящая этот отрезок в отношении 4 : 5 , считая от В. Найти, в каком отношении прямая AK делит сторону BC.
Решение: Обозначим точкой Х точку пересечения АК и ВС. Проведем через В1 прямую параллельную АХ. Если смотреть на стороны угла C, то с нижней стороны отношение 3 : 2 проектируется на ВС. Обозначим тогда отрезки 2a и 3a. А теперь, глядя на угол с вершиной B треугольника ВВ1С, раз на отрезке BB1 верхний кусок составляет 4: 5 от нижнего, то и на ВС верхний кусок составляет 4: 5 от 3a , т. е. (12:5) a. Следовательно, BX : XC = (12:5)а/(3а + 2а) = 12:25.
Интересно заметить тут, что задачу можно было решить и другим способом. С помощью теоремы Менелая. Эта теорема в школьном курсе не рассматривается, учебник предлагает рассмотреть ее в форме реферата для учащихся. Кстати, это еще один способ заинтересовать учащихся: дать возможность им самим доказать эти теоремы в форме проектной работы.
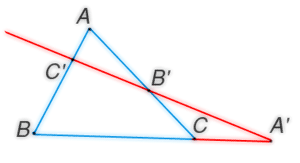
Теорема Менелая: Если точки А1 ,В1, С1 лежат соответственно на сторонах ВС, АС и АВ треугольника АВС или на их продолжениях, то выполняется равенство: (ВС1 : С1А)(АВ1 : В1С )(СА1 : А1В) = 1.
Вернемся теперь к задаче.
Если рассмотреть треугольник ВВ1С и прямую АХ и составить отношение длин отрезков, то мы получаем, что (СХ : ХВ)(ВК : КВ1)(В1А : АС) = 1 подставляя в это равенство известные отношения (СХ : ХВ)(4 : 5)(3 : 5) = 1 получаем что СХ : ХВ = 25 : 12, а ВХ : ХС = 12 : 25.
Перед тем как давать следующую задачу учащимся предлагается рассмотреть три вспомогательных утверждения с доказательством.
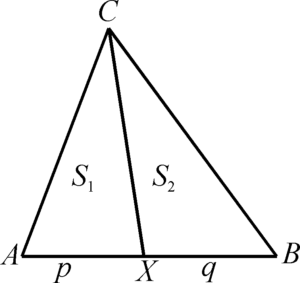
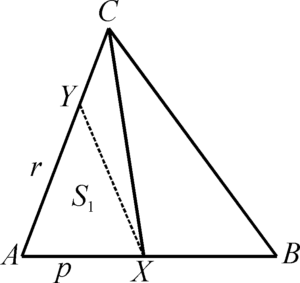
Теорема 1: Если точка X делит сторону AB треугольника ABC в отношении p:q, то отрезок CX делит треугольник на части, отношение площадей которых также равно p : q , т. е. S1 : S2 = p : q.
Другая формулировка этой теоремы в учебнике звучит так: если треугольники имеют общую высоту, то их площади относятся как основания.
Теорема 2: Если на сторонах AB и AC треугольника ABC расположены точки X и Y так, что отсекаемые отрезки составляют p-ю и r-ю долю соответствующих сторон, то площадь отрезаемого треугольника AXY составляет (pr)-ю долю площади ABC. SАХY = pr S0 .
Доказать можно легко использую формулу площади треугольника как полупроизведение сторон на синус угла между ними.
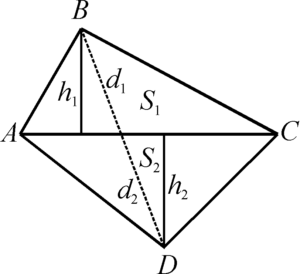
Теорема 3: Если четырехугольник ABCD разрезан диагональю AC на два треугольника: ABC площадью S1 и ADC площадью S2 , то эти площади относятся друг к другу так же, как куски второй диагонали d1 и d2 , содержащиеся внутри этих треугольников: S1 : S2 = d1 : d2 .
Для доказательства достаточно заметить, что у верхнего и нижнего треугольника за основание можно взять один и тот же отрезок AC. Но тогда их площади относятся как их высоты h1 и h2 . А эти высоты относятся как d1 к d2 ,
что следует из подобия прямоугольных треугольников, где высоты являются катетами, а d1 и d2 гипотенузами.
Рассмотрим еще однузадачу.
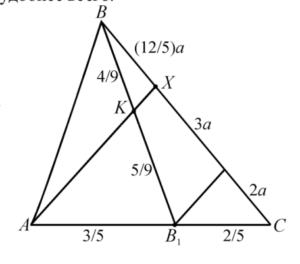
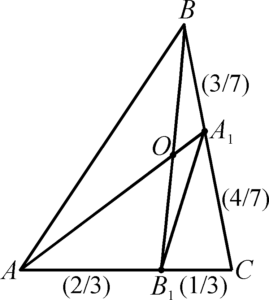
Задача 2: В треугольнике ABC точка A1 лежит на стороне BC, точка B1 на стороне AC, причем BA1 : A1C = 3 : 4 ;
AB1 : B1C = 2 :1 . Отрезки AA1 и BB1 пересекаются в точке O. Найти, в каком от-
ношении точка O делит отрезок AA1 .
Решение: Заметим, что эту задачу можно решить по теореме Фалеса и по теореме Менелая. Теперь попробуем решить ее с помощью площадей.
Построим четырехугольник AB1A1B, соединив точки A1 и B1. Нам нужно найти AO : OA1, но по теореме 3 это отношение
равно SВВ1А : SВВ1А1 . Площадь первого равна (2 : 3)S0 (по теореме 1, где S0 площадь треугольника АВС), а площадь второго по той же теореме равна (3:7) площади треугольника
BB1C , которая есть (1: 3) S0 . То есть (1:7)S0 . Итого, ОА : ОА1 = (2:3)/(1:7) = 14:3.
Перечислю еще несколько интересных утверждений, которые можно дать ребятам в качестве проектной деятельности: точка Микеля, точка Жергона, точка Нагеля, точка Брокара, теорема Паскаля, теорема Птолемея, теорема Чевы, прямая Эйлера, прямая Симсона. Ели учитель разработает цикл задач в решении которых используются эти утверждения, то учащиеся без сомнения будут не только развиваться но и занимать призовые места в различных геометрических олимпиадах.
Библиографический список:
1. Геометрические олимпиады им. И. Ф. Шарыгина / Сост. А. А. Заславский, В. Ю. Протасов, Д. И. Шарыгин. — М.:МЦНМО, 2007. — 152 с.
2. Бубнова Н.А., Платонова О.А., Хаханян В.Х. – Геометрические и нестандартные задачи по элементарной математике. Учебное пособие. Под ред. О.А. Платоновой. – М.: МИИТ, 2014. – 138 с.
3. Воронин В. В. Метод. пособие: Отношения отрезков и площадей. Новосибирск: НГУ, 2016. — 40 с.
4. Прасолов В. В. Задачи по планиметрии: Учебное пособие. — 5-е изд., испр. и доп. — М.: МЦНМО: ОАО «Московские учебники», 2006. — 640 с.